Segi tiga voltan, rintangan dan kuasa

Sesiapa yang mempunyai idea tentang gambar rajah vektor akan dengan mudah melihat bahawa segitiga voltan bersudut tepat boleh dibezakan dengan jelas pada mereka, setiap sisinya mencerminkan: jumlah voltan litar, voltan rintangan aktif dan voltan pada reaktans.

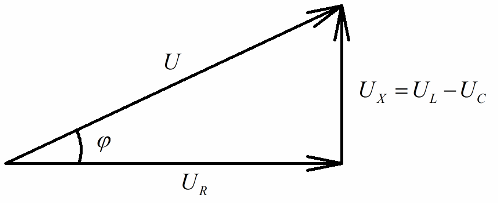
Selaras dengan teorem Pythagoras, hubungan antara voltan ini (antara jumlah voltan litar dan voltan bahagiannya) akan kelihatan seperti ini:

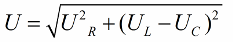
Jika langkah seterusnya ialah membahagikan nilai voltan ini dengan arus (arus mengalir melalui semua bahagian litar siri secara sama rata), maka dengan Hukum Ohm kita mendapat nilai rintangan, iaitu, sekarang kita boleh bercakap tentang segi tiga bersudut tegak rintangan:

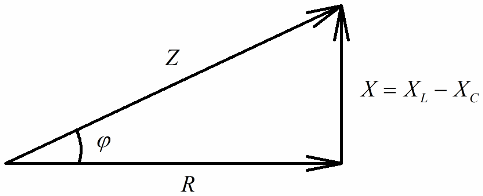
Dengan cara yang sama (seperti dalam kes voltan), menggunakan teorem Pythagoras, adalah mungkin untuk mewujudkan hubungan antara impedans litar dan reaktans. Hubungan itu akan dinyatakan dengan formula berikut:

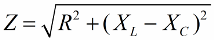
Kemudian kita mendarabkan nilai rintangan dengan arus, sebenarnya kita akan meningkatkan setiap sisi segi tiga tepat dengan bilangan kali tertentu. Akibatnya, kami mendapat segi tiga bersudut tegak dengan kapasiti:

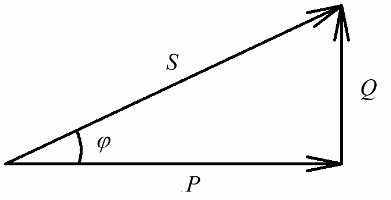
Kuasa aktif yang dilepaskan pada rintangan aktif litar yang berkaitan dengan penukaran tenaga elektrik yang tidak dapat dipulihkan (ke dalam haba, dalam prestasi kerja dalam pemasangan) akan jelas berkaitan dengan kuasa reaktif yang terlibat dalam penukaran tenaga boleh balik (penciptaan medan magnet dan elektrik dalam gegelung dan kapasitor) dan dengan kuasa penuh yang dibekalkan kepada pemasangan elektrik.

Kuasa aktif diukur dalam watt (W), kuasa reaktif — dalam varis (VAR — volt-ampere reaktif), jumlah — dalam VA (volt-ampere).

Menurut teorem Pythagoras, kita mempunyai hak untuk menulis:

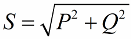
Sekarang mari kita perhatikan fakta bahawa dalam segi tiga kuasa terdapat sudut phi, kosinus yang mudah ditentukan terutamanya oleh kuasa aktif dan kuasa ketara. Kosinus sudut ini (cos phi) dipanggil faktor kuasa. Ia menunjukkan berapa banyak daripada jumlah kuasa yang diambil kira apabila melakukan kerja berguna dalam pemasangan elektrik dan tidak dikembalikan ke grid.

Jelas sekali, faktor kuasa yang lebih tinggi (maksimum satu) menunjukkan kecekapan penukaran yang lebih tinggi bagi tenaga yang dihantar ke loji untuk operasi. Jika faktor kuasa adalah 1, maka semua tenaga yang dibekalkan digunakan untuk melakukan kerja.

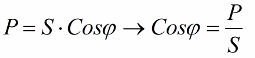
Nisbah yang diperoleh membenarkan ungkapan penggunaan semasa pemasangan dari segi faktor kuasa, kuasa aktif dan voltan rangkaian:

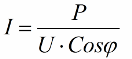
Jadi, lebih kecil kosinus phi, lebih banyak arus yang diperlukan oleh rangkaian untuk melakukan kerja tertentu. Dalam amalan, faktor ini (arus rangkaian maksimum) mengehadkan kapasiti penghantaran talian penghantaran dan oleh itu, semakin rendah faktor kuasa, semakin besar beban talian dan semakin rendah lebar jalur yang berguna (phi kosinus yang rendah membawa kepada sekatan ). Kehilangan joule dalam talian kuasa dengan penurunan phi kosinus boleh dilihat daripada formula berikut:

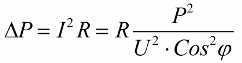
Pada rintangan aktif R talian penghantaran, kerugian meningkat semakin tinggi arus I, walaupun ia reaktif kepada beban. Oleh itu, kita boleh mengatakan bahawa dengan faktor kuasa yang rendah, kos penghantaran elektrik hanya meningkat. Ini bermakna peningkatan phi kosinus adalah tugas ekonomi negara yang penting.

Adalah wajar bahawa komponen reaktif bagi jumlah kuasa harus mendekati sifar. Untuk melakukan ini, adalah baik untuk sentiasa menggunakan motor elektrik dan transformer pada beban penuh dan mematikannya pada akhir penggunaan supaya ia tidak melahu. Tanpa beban, motor dan transformer mempunyai faktor kuasa yang sangat rendah. Satu cara untuk meningkatkan phi kosinus dalam pengguna adalah dengan menggunakan bank kapasitor dan pemampas segerak.