Resonans voltan
Jika litar AC disambung secara bersiri induktor dan kapasitor, maka mereka dengan cara mereka sendiri mempengaruhi penjana yang menyuap litar dan sambungan fasa antara arus dan voltan.
Induktor memperkenalkan anjakan fasa di mana arus ketinggalan voltan sebanyak suku tempoh, manakala kapasitor, sebaliknya, menjadikan voltan dalam litar ketinggalan arus sebanyak suku tempoh. Oleh itu, kesan rintangan induktif pada peralihan fasa antara arus dan voltan dalam litar adalah bertentangan dengan kesan rintangan kapasitif.
Ini membawa kepada fakta bahawa jumlah peralihan fasa antara arus dan voltan dalam litar bergantung kepada nisbah nilai rintangan induktif dan kapasitif.
Jika nilai rintangan kapasitif litar lebih besar daripada induktif, maka litar itu bersifat kapasitif, iaitu, voltan ketinggalan di belakang arus dalam fasa. Jika, sebaliknya, rintangan induktif litar lebih besar daripada kapasitif, maka voltan membawa arus dan oleh itu litar adalah induktif.
Jumlah reaktans Xtot litar yang sedang kita pertimbangkan ditentukan dengan menambah rintangan induktif gegelung XL dan rintangan kapasitif kapasitor XC.
Tetapi kerana tindakan rintangan ini dalam litar adalah bertentangan, maka salah satu daripadanya, iaitu Xc, diberikan tanda tolak, dan jumlah reaktans ditentukan oleh formula:
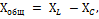
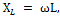
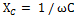
Sapukan pada litar ini Hukum Ohm, kita mendapatkan:
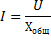
Formula ini boleh diubah seperti berikut:
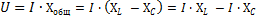
Dalam persamaan yang terhasil, AzxL — nilai berkesan komponen jumlah voltan litar, yang akan mengatasi rintangan induktif litar, dan AzNSC — nilai berkesan komponen jumlah voltan litar, yang akan mengatasi rintangan kapasitif.
Oleh itu, jumlah voltan litar yang terdiri daripada sambungan siri gegelung dan kapasitor boleh dianggap sebagai terdiri daripada dua sebutan, nilainya bergantung pada nilai rintangan induktif dan kapasitif bagi litar.
Kami percaya bahawa litar sedemikian tidak mempunyai rintangan aktif. Walau bagaimanapun, dalam kes di mana rintangan aktif litar tidak lagi begitu kecil sehingga boleh diabaikan, jumlah rintangan litar ditentukan oleh formula berikut:
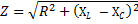
di mana R ialah jumlah rintangan aktif litar, XL -NSC — jumlah reaktansnya. Bergerak ke formula hukum Ohm, kami mempunyai hak untuk menulis:
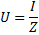
resonans voltan AC
Rintangan induktif dan kapasitif yang disambungkan secara bersiri menyebabkan kurang peralihan fasa antara arus dan voltan dalam litar AC berbanding jika ia dimasukkan ke dalam litar secara berasingan.
Dalam erti kata lain, daripada tindakan serentak kedua-dua tindak balas yang berbeza sifat dalam litar, pampasan (kemusnahan bersama) anjakan fasa berlaku.
Pampasan penuh, iaitu. penghapusan lengkap peralihan fasa antara arus dan voltan dalam litar sedemikian akan berlaku apabila rintangan induktif adalah sama dengan rintangan kapasitif litar, iaitu apabila XL = XC atau, yang sama, apabila ωL = 1 / ωC.
Dalam kes ini, litar akan berkelakuan sebagai rintangan aktif semata-mata, iaitu, seolah-olah ia tidak mempunyai gegelung mahupun kapasitor. Nilai rintangan ini ditentukan oleh jumlah rintangan aktif gegelung dan wayar penyambung. Di mana arus berkesan dalam litar akan menjadi yang terbesar dan ditentukan oleh formula hukum Ohm I = U / R di mana Z kini digantikan oleh R.
Pada masa yang sama, voltan yang bertindak pada gegelung UL = AzxL dan pada kapasitor Uc = AzNSCC akan sama dan akan menjadi sebesar mungkin. Dengan rintangan aktif litar yang rendah, voltan ini boleh berkali-kali melebihi jumlah voltan U terminal litar. Fenomena menarik ini dipanggil resonans voltan dalam kejuruteraan elektrik.
Dalam rajah. 1 menunjukkan lengkung voltan, arus dan kuasa pada voltan resonans dalam litar.
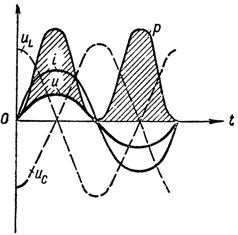
Graf arus voltan dan kuasa pada resonans voltan
Perlu diingat bahawa rintangan XL dan C adalah pembolehubah yang bergantung pada frekuensi arus dan ia bernilai sekurang-kurangnya mengubah frekuensinya, sebagai contoh, meningkatkannya kerana XL = ωL akan meningkat, dan XSC = = 1 / ωC akan berkurangan dan dengan itu resonans voltan dalam litar akan serta-merta terganggu, manakala bersama-sama dengan rintangan aktif, reaktans akan muncul dalam litar. Perkara yang sama akan berlaku jika anda menukar nilai kearuhan atau kemuatan litar.
Dengan resonans voltan, kuasa sumber arus akan dibelanjakan hanya untuk mengatasi rintangan aktif litar, iaitu, untuk memanaskan wayar.
Malah, dalam litar dengan gegelung induktif tunggal, turun naik tenaga berlaku, i.e. pemindahan tenaga secara berkala daripada penjana ke medan magnet gegelung. Dalam litar dengan kapasitor, perkara yang sama berlaku, tetapi kerana tenaga medan elektrik kapasitor. Dalam litar dengan kapasitor dan induktor pada resonans voltan (ХL = XС), tenaga, setelah disimpan oleh litar, secara berkala melewati dari gegelung ke kapasitor dan sebaliknya, dan hanya penggunaan tenaga yang diperlukan untuk mengatasi rintangan aktif litar jatuh pada bahagian punca arus. Oleh itu, pertukaran tenaga berlaku antara kapasitor dan gegelung hampir tanpa penyertaan penjana.
Seseorang hanya perlu memecahkan resonans voltan mengikut nilai, bagaimana tenaga medan magnet gegelung menjadi tidak sama dengan tenaga medan elektrik kapasitor, dan dalam proses pertukaran tenaga antara medan ini, lebihan tenaga akan muncul, yang secara berkala akan mengalir keluar dari sumber dalam litar, kemudian suapan semula kepadanya dalam litar.
Fenomena ini hampir sama dengan apa yang berlaku dalam kerja jam. Bandul jam akan dapat berayun secara berterusan tanpa bantuan spring (atau pemberat dalam pejalan jam) jika bukan kerana daya geseran yang memperlahankan pergerakannya.
Spring, dengan menghantar sebahagian tenaganya ke bandul pada masa yang tepat, membantunya mengatasi daya geseran, dengan itu mencapai kesinambungan ayunan.
Begitu juga, dalam litar elektrik, apabila resonans berlaku di dalamnya, sumber arus menghabiskan tenaganya hanya untuk mengatasi rintangan aktif litar, dengan itu membantu proses berayun di dalamnya.
Oleh itu kita sampai pada kesimpulan bahawa litar arus ulang-alik, yang terdiri daripada penjana dan induktor dan kapasitor bersambung siri, dalam keadaan tertentu XL = XС menjadi sistem berayun... Litar ini dinamakan litar berayun.
Dari persamaan XL = XC adalah mungkin untuk menentukan nilai frekuensi penjana di mana fenomena resonans voltan berlaku:
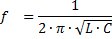
Maksud kemuatan dan kearuhan litar di mana resonans voltan berlaku:
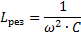
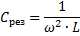
Oleh itu, menukar mana-mana daripada tiga kuantiti ini (eres, L dan C), adalah mungkin untuk menyebabkan resonans voltan dalam litar, iaitu, mengubah litar menjadi litar berayun.
Contoh aplikasi berguna resonans voltan: Litar input penerima dilaraskan oleh kapasitor boleh ubah (atau variometer) sedemikian rupa sehingga resonans voltan berlaku di dalamnya. Ini mencapai peningkatan besar dalam voltan gegelung yang diperlukan untuk operasi penerima biasa berbanding voltan litar yang dicipta oleh antena.
Bersama-sama dengan penggunaan berguna fenomena resonans voltan dalam kejuruteraan elektrik, sering terdapat kes di mana resonans voltan berbahaya. Peningkatan besar dalam voltan dalam bahagian individu litar (pada gegelung atau pada kapasitor) berbanding voltan daripada penjana boleh menyebabkan kerosakan bahagian berasingan dan alat pengukur.

