Resonans arus

Sambungan selari kapasitor dan induktor dalam litar arus ulang-alik

Pertimbangkan fenomena dalam rantaian arus ulang alikmengandungi penjana, kapasitor dan induktor yang disambung secara selari. Andaikan bahawa litar tidak mempunyai rintangan aktif.

Jelas sekali, dalam litar sedemikian voltan kedua-dua gegelung dan kapasitor pada bila-bila masa adalah sama dengan voltan yang dibangunkan oleh penjana.

Jumlah arus dalam litar terdiri daripada arus di cawangannya. Arus dalam cawangan induktif ketinggalan voltan dalam fasa sebanyak satu perempat daripada tempoh, dan arus dalam cawangan kapasitif membawanya dengan suku yang sama tempoh. Oleh itu, arus dalam cawangan pada bila-bila masa berubah menjadi fasa-anjakan relatif antara satu sama lain dengan separuh tempoh, iaitu, ia berada dalam antifasa. Oleh itu, arus dalam cawangan pada bila-bila masa diarahkan ke arah satu sama lain, dan jumlah arus di bahagian litar yang tidak bercabang adalah sama dengan perbezaannya.

Ini memberi kita hak untuk menulis kesamaan I = IL -litar bersepadu

di mana saya- nilai berkesan jumlah arus dalam litar, I L dan litar bersepadu — nilai berkesan arus di cawangan.

Menggunakan undang-undang Ohm untuk menentukan nilai berkesan arus di cawangan, kami mendapat:

Il = U / XL dan Az° C = U / XC

Jika litar dikuasai oleh rintangan induktif, iaitu. XL Lebih ▼ XC, arus dalam gegelung adalah kurang daripada arus dalam kapasitor; oleh itu arus dalam bahagian litar yang tidak bercabang adalah bersifat kapasitif dan litar secara keseluruhan untuk penjana akan menjadi kapasitif. Sebaliknya, dengan XC lebih besar daripada XL, arus dalam kapasitor adalah kurang daripada arus dalam gegelung; oleh itu arus dalam bahagian litar yang tidak bercabang adalah induktif, dan litar secara keseluruhan untuk penjana akan menjadi induktif.

Ia tidak boleh dilupakan bahawa dalam kedua-dua kes beban adalah reaktif, i.e. litar tidak menggunakan kuasa penjana.

Resonans arus

Sekarang mari kita pertimbangkan kes apabila kapasitor dan gegelung yang disambungkan secara selari ternyata sama dalam reaktansnya, i.e. XlL = X°C.

Jika, seperti sebelum ini, kita mengandaikan bahawa gegelung dan kapasitor tidak mempunyai rintangan aktif, maka jika tindak balas mereka adalah sama (YL = Y° C) jumlah arus di bahagian litar yang tidak bercabang akan menjadi sifar, manakala di cawangan sama. arus akan mengalir dengan magnitud yang paling besar. Dalam kes ini, fenomena arus resonans berlaku dalam litar.

Pada resonans semasa, nilai berkesan arus dalam setiap cawangan, ditentukan oleh nisbah IL = U / XL dan Аz° С = U / XC akan sama antara satu sama lain, supaya XL = XC.

Kesimpulan yang kami capai mungkin kelihatan agak pelik pada pandangan pertama. Malah, penjana dimuatkan dengan dua rintangan dan tiada arus di bahagian litar yang tidak bercabang, manakala sama dan, lebih-lebih lagi, arus terbesar mengalir dalam rintangan itu sendiri.

Ini dijelaskan oleh kelakuan medan magnet gegelung dan medan elektrik kapasitor… Pada resonans arus, seperti dalam resonans voltan, terdapat turun naik tenaga antara medan gegelung dan medan kapasitor. Penjana, selepas menyampaikan tenaga kepada litar, nampaknya terpencil. Ia boleh dimatikan sepenuhnya dan arus di bahagian bercabang litar akan dikekalkan tanpa penjana oleh tenaga yang disimpan oleh litar pada mulanya. Juga, voltan merentasi terminal litar akan kekal sama seperti yang dibangunkan oleh penjana.

Oleh itu, apabila induktor dan kapasitor disambung secara selari, kami memperoleh litar pengayun yang berbeza daripada yang diterangkan di atas hanya kerana penjana yang mencipta ayunan tidak disambungkan terus ke litar dan litar ditutup. 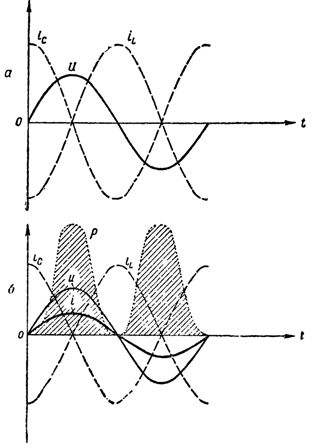Graf arus, voltan dan kuasa dalam litar pada resonans arus: a — rintangan aktif adalah sama dengan sifar, litar tidak menggunakan tenaga; b — litar mempunyai rintangan aktif, arus telah muncul di bahagian litar yang tidak bercabang, litar menggunakan tenaga

L, C dan e, di mana resonans semasa berlaku, ditentukan, seperti dalam resonans voltan (jika kita mengabaikan rintangan aktif litar), dengan kesamaan:

ωL = 1 / ω° C

Oleh itu:

eres = 1 / 2π√LC

Lres = 1 / ω2C

Sekeping = 1 / ω2L

Dengan menukar mana-mana daripada tiga kuantiti ini, kesamaan Xl = X° C boleh dicapai, iaitu mengubah litar menjadi litar berayun.

Jadi, kita mempunyai litar berayun tertutup di mana kita boleh mendorong ayunan elektrik, i.e. arus ulang alik. Dan jika bukan kerana rintangan aktif yang dimiliki oleh setiap litar berayun, arus ulang alik mungkin terus wujud di dalamnya.Kehadiran rintangan aktif membawa kepada fakta bahawa ayunan dalam litar secara beransur-ansur mati, dan untuk mengekalkannya, sumber tenaga diperlukan - alternator.

Dalam litar arus bukan sinusoidal, mod resonans mungkin untuk pelbagai komponen harmonik.

Arus resonan digunakan secara meluas dalam amalan. Fenomena resonans semasa digunakan dalam penapis laluan jalur sebagai "pengapit" elektrik yang melambatkan frekuensi tertentu. Oleh kerana terdapat rintangan arus yang ketara pada frekuensi f, penurunan voltan dalam litar pada frekuensi f akan menjadi maksimum. Sifat gelung ini dipanggil selektiviti, ia digunakan dalam penerima radio untuk mengasingkan isyarat stesen radio tertentu. Litar berayun yang beroperasi dalam mod arus resonan adalah salah satu komponen utama penjana elektronik.