Ayunan berterusan dan resonans parametrik

Getaran berterusan — getaran yang tenaganya tidak berubah dari semasa ke semasa. Dalam sistem fizikal sebenar, sentiasa ada punca yang menyebabkan peralihan tenaga getaran kepada tenaga haba (contohnya geseran dalam sistem mekanikal, rintangan aktif dalam sistem elektrik).

Oleh itu, ayunan tidak lembap hanya boleh diperolehi dengan syarat kehilangan tenaga ini diisi semula. Pengisian semula sedemikian berlaku secara automatik dalam sistem berayun sendiri disebabkan tenaga daripada sumber luaran. Ayunan elektromagnet berterusan digunakan secara meluas. Penjana yang berbeza digunakan untuk mendapatkannya.

Untuk membuat getaran elektrik atau mekanikal (daripada bulatan berayun atau bandul) tidak terendam, adalah perlu untuk mengimbangi rintangan atau kehilangan geseran pada setiap masa.

Sebagai contoh, anda boleh bertindak pada litar berayun dengan EMF berselang-seli, yang secara berkala akan meningkatkan arus dalam gegelung dan, dengan itu, mengekalkan amplitud voltan dalam kapasitor.Atau anda boleh menolak bandul dengan cara yang sama, memastikan ia berayun harmoni.

Seperti yang anda ketahui, magnitud tenaga medan magnet gegelung litar berayun berkaitan dengan kearuhan dan arusnya dengan hubungan berikut (rumus kedua ialahtenaga medan elektrik pemuat kontur kontur yang sama)

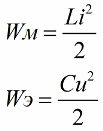
Jelas dari formula pertama bahawa jika kita secara berkala meningkatkan arus dalam gegelung, bertindak pada litar EMF berselang-seli, maka (dengan menambah atau mengurangkan faktor kedua dalam formula - arus) kita akan mengisi semula litar ini dengan tenaga secara berkala.

Bertindak pada litar dengan tepat pada masanya dengan ayunan bebas semulajadi, iaitu, pada frekuensi resonans, kita akan mendapat fenomena resonans elektrik, kerana ia berada pada frekuensi resonans sistem berayun paling intensif menyerap tenaga yang dibekalkan kepadanya.

Tetapi bagaimana jika anda secara berkala menukar bukan faktor kedua (bukan semasa atau voltan), tetapi faktor pertama - kearuhan atau kapasitansi? Dalam kes ini, litar juga akan mengalami perubahan dalam tenaganya.

Contohnya, secara berkala menolak teras masuk dan keluar dari gegelung atau menolak masuk dan keluar dari kapasitordielektrik, — kita juga mendapat perubahan berkala yang sangat pasti dalam tenaga dalam litar.

Kami menulis kedudukan ini untuk perubahan unit dalam kearuhan gegelung:

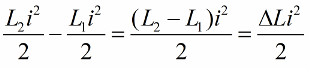
Kesan ayunan litar yang paling ketara adalah jika perubahan induktansi dibuat tepat pada masanya. Sebagai contoh, jika kita mengambil litar yang sama pada bila-bila masa, apabila beberapa arus i sudah mengalir melaluinya, dan memasukkan teras ke dalam gegelung, maka tenaga akan berubah mengikut jumlah berikut:

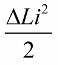
Sekarang biarkan ayunan bebas muncul dalam litar itu sendiri, tetapi pada masa ini, selepas tempoh suku, tenaga telah sepenuhnya masuk ke dalam kapasitor dan arus dalam gegelung telah menjadi sifar, kami akan mengeluarkan teras dari gegelung secara tiba-tiba. akan kembali ke keadaan asalnya, kepada nilai awal L. Tiada kerja yang perlu dibelanjakan terhadap medan magnet apabila teras dibuang. Oleh itu, apabila teras ditolak ke dalam gegelung, litar menerima tenaga, kerana kami bekerja, nilainya:

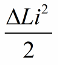
Selepas satu perempat tempoh, kapasitor mula menyahcas, tenaganya sekali lagi ditukar kepada tenaga medan magnet gegelung.Apabila medan magnet mencapai amplitud, kami akan menekan teras secara mendadak sekali lagi. Sekali lagi induktansi meningkat, meningkat dengan jumlah yang sama.

Dan sekali lagi, pada arus sifar, kami mengembalikan induktansi kepada nilai asalnya. Akibatnya, jika keuntungan tenaga bagi setiap separuh kitaran melebihi kehilangan rintangan, tenaga gelung akan meningkat sepanjang masa dan amplitud ayunan akan meningkat. Keadaan ini dinyatakan oleh ketidaksamaan:

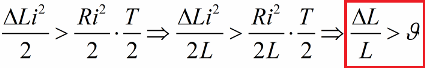
Di sini kami membahagikan kedua-dua belah ketaksamaan ini dengan L dan menuliskan syarat untuk kemungkinan pengujaan parametrik dengan lompatan untuk nilai penurunan logaritma tertentu.

Adalah disyorkan untuk menukar induktansi (atau kapasitans) dua kali setiap tempoh, oleh itu kekerapan perubahan parameter (frekuensi resonans parametrik) hendaklah dua kali ganda frekuensi semula jadi sistem berayun:

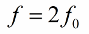
Jadi laluan pengujaan ayunan dalam litar telah muncul tanpa perlu menukar EMF atau arus secara langsung.Arus turun naik awal dalam litar sentiasa hadir dalam satu cara atau yang lain, dan itu tidak mengambil kira gangguan daripada ayunan frekuensi radio di atmosfera.

Sekiranya induktansi (atau kapasitansi) tidak berubah dalam lompatan, tetapi secara harmoni, maka keadaan untuk terjadinya ayunan akan kelihatan sedikit berbeza:

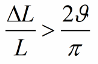
Oleh kerana kemuatan dan kearuhan ialah parameter litar (seperti jisim bandul atau keanjalan spring), kaedah ayunan yang menarik juga dipanggil pengujaan parametrik.

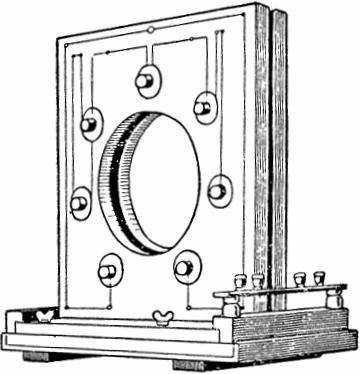
Fenomena ini ditemui dan dikaji secara praktikal pada awal abad ke-20 oleh ahli fizik Soviet Mandelstam dan Papalexi. Berdasarkan fenomena fizikal ini, mereka membina penjana AC parametrik pertama dengan kuasa 4 kW dan kearuhan berubah-ubah.

Dalam reka bentuk penjana, tujuh pasang gegelung rata terletak di kedua-dua belah bingkai, di dalam rongga yang cakera feromagnetik dengan tonjolan berputar. Apabila cakera didorong untuk berputar oleh motor, tonjolannya secara berkala bergerak masuk dan keluar dari ruang antara setiap pasangan gegelung, dengan itu mengubah kearuhan dan ayunan yang menarik.