Arus impuls

Dalam pelbagai peranti elektronik, sebagai contoh, dalam peralatan elektronik dan semikonduktor, iaitu dalam penguat, penerus, radio, penjana, televisyen, serta dalam mikrofon karbon, telegraf dan banyak peranti lain, ia digunakan secara meluas arus dan voltan riak... Agar untuk tidak mengulangi alasan dua kali, kita hanya akan bercakap tentang arus, tetapi semua yang berkaitan dengan arus juga benar untuk voltan.

Arus berdenyut yang mempunyai arah tetap tetapi mengubah nilainya boleh berbeza. Kadangkala nilai semasa berubah daripada nilai tertinggi kepada nilai bukan sifar terendah. Dalam kes lain, arus dikurangkan kepada sifar. Jika litar arus terus terganggu pada frekuensi tertentu, maka untuk beberapa selang masa tiada arus dalam litar.

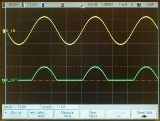
Dalam rajah. 1 menunjukkan graf pelbagai arus gelombang. Dalam rajah. 1, a, b, perubahan arus berlaku mengikut lengkung sinusoidal, tetapi arus ini tidak boleh dianggap sebagai arus ulang alik sinusoidal, kerana arah (tanda) arus tidak berubah. Dalam rajah.1, c menunjukkan arus yang terdiri daripada denyutan berasingan, iaitu, "kejutan" jangka pendek arus, dipisahkan antara satu sama lain dengan jeda tempoh yang lebih besar atau lebih kecil, dan sering dipanggil arus berdenyut. Arus denyutan yang berbeza berbeza antara satu sama lain dalam bentuk dan tempoh denyutan, serta dalam kadar pengulangan.

Adalah mudah untuk mempertimbangkan sebarang jenis arus berdenyut sebagai jumlah dua arus - terus dan berselang-seli, dipanggil arus jangka atau komponen. Sebarang arus berdenyut mempunyai komponen DC dan AC. Ini kelihatan pelik kepada ramai. Malah, selepas semua, arus berdenyut adalah arus yang mengalir sepanjang masa dalam satu arah dan mengubah nilainya.

Bagaimanakah anda boleh memberitahu ia mengandungi arus ulang alik yang mengubah arah? Walau bagaimanapun, jika dua arus - terus dan berselang-seli - melepasi secara serentak melalui wayar yang sama, ternyata arus berdenyut akan mengalir dalam wayar itu (Rajah 2). Dalam kes ini, amplitud arus ulang alik tidak boleh melebihi nilai arus terus. Arus terus dan arus ulang alik tidak boleh mengalir secara berasingan melalui wayar. Mereka menambah kepada aliran umum elektron yang mempunyai semua sifat arus berdenyut.

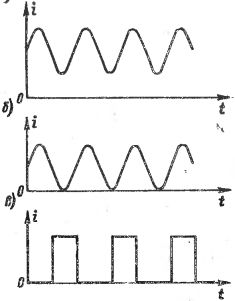
nasi. 1. Graf pelbagai arus gelombang

Penambahan arus AC dan DC boleh ditunjukkan secara grafik. Dalam rajah. 2 menunjukkan graf arus terus bersamaan dengan 15 mA dan arus ulang alik dengan amplitud 10 mA. Jika kita menjumlahkan nilai arus ini untuk titik individu dalam masa, dengan mengambil kira arah (tanda) arus, kita mendapat graf arus gelombang yang ditunjukkan dalam rajah. 2 dengan garis tebal. Arus ini berbeza dari rendah 5 mA hingga tinggi 25 mA.

Penambahan arus yang dipertimbangkan mengesahkan kesahihan perwakilan arus berdenyut sebagai jumlah arus terus dan arus ulang alik. Ketepatan perwakilan ini juga disahkan oleh fakta bahawa dengan bantuan beberapa peranti adalah mungkin untuk memisahkan komponen arus ini antara satu sama lain.

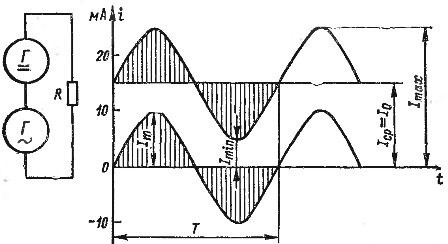
nasi. 2. Mendapatkan arus berdenyut dengan menambah arus terus dan ulang alik.

Perlu ditekankan bahawa sebarang arus sentiasa boleh diwakili sebagai jumlah beberapa arus. Sebagai contoh, arus 5 A boleh dianggap sebagai jumlah arus 2 dan 3 A yang mengalir dalam satu arah, atau jumlah arus 8 dan 3 A yang mengalir dalam arah yang berbeza, iaitu, dengan kata lain, perbezaan antara arus 8 dan 3 A. Tidak sukar untuk mencari gabungan lain dua atau lebih arus yang memberikan jumlah 5 A.

Di sini terdapat persamaan lengkap dengan prinsip penambahan dan penguraian daya. Jika dua daya yang sama diarahkan bertindak ke atas sebarang objek, ia boleh digantikan dengan satu daya sepunya. Daya yang bertindak dalam arah yang bertentangan boleh digantikan dengan perbezaan unit. Sebaliknya, daya yang diberikan sentiasa boleh dianggap sebagai jumlah daya yang sama diarahkan atau perbezaan antara daya yang diarahkan bertentangan.

Ia tidak perlu menguraikan arus ulang alik terus atau sinusoidal kepada arus komponen. Jika kita menggantikan arus berdenyut dengan jumlah arus terus dan arus ulang alik, maka dengan menggunakan undang-undang arus terus dan ulang alik yang diketahui kepada arus komponen ini, adalah mungkin untuk menyelesaikan banyak masalah dan membuat pengiraan yang diperlukan berkaitan dengan arus berdenyut.

Konsep arus berdenyut sebagai jumlah arus terus dan arus ulang alik adalah konvensional.Sudah tentu, ia tidak boleh diandaikan bahawa pada selang masa tertentu arus terus dan arus ulang alik benar-benar mengalir ke arah satu sama lain di sepanjang wayar. Sebenarnya, tiada dua aliran elektron yang bertentangan.

Pada hakikatnya, arus berdenyut adalah arus tunggal yang mengubah nilainya dari semasa ke semasa. Adalah lebih tepat untuk mengatakan bahawa voltan berdenyut atau EMF berdenyut boleh diwakili sebagai jumlah komponen malar dan berubah-ubah.

Sebagai contoh, dalam FIG. 2 menunjukkan bagaimana secara algebra emf pemalar satu penjana ditambah kepada emf pembolehubah penjana yang lain. Akibatnya, kita mempunyai EMF berdenyut yang menyebabkan arus berdenyut yang sepadan. Secara bersyarat, bagaimanapun, boleh dianggap bahawa EMF malar mencipta arus terus dalam litar, dan EMF berselang-seli - arus ulang-alik, yang, apabila dijumlahkan, membentuk arus berdenyut.

Setiap arus berdenyut boleh dicirikan oleh nilai maksimum dan minimum Itax dan Itin, serta komponen malar dan berubah-ubahnya. Komponen malar dilambangkan dengan I0. Jika komponen berselang-seli ialah arus sinusoidal, maka amplitudnya dilambangkan dengan Ia (semua kuantiti ini ditunjukkan dalam Rajah 2).

Ia tidak sepatutnya dikelirukan dengan It dan Itax. Juga, nilai maksimum gelombang semasa Imax tidak boleh dipanggil amplitud. Istilah amplitud biasanya hanya merujuk kepada arus ulang alik. Mengenai arus berdenyut, kita hanya boleh bercakap tentang amplitud komponen pembolehubahnya.

Komponen malar arus berdenyut boleh dipanggil nilai purata Iav, iaitu nilai purata aritmetik. Sesungguhnya, jika kita mempertimbangkan perubahan dalam satu tempoh arus berdenyut yang ditunjukkan dalam Rajah.2, perkara berikut dapat dilihat dengan jelas: dalam separuh kitaran pertama, beberapa nilai ditambah kepada arus 15 mA dengan mengubah komponen semasa, berbeza dari 0 hingga 10 mA dan kembali ke 0, dan pada separuh kedua -kitaran, nilai semasa yang sama ditolak daripada 15 mA semasa.

Oleh itu, arus 15 mA benar-benar nilai purata. Oleh kerana arus ialah pemindahan cas elektrik melalui keratan rentas wayar, maka Iav ialah nilai arus terus sedemikian yang dalam satu tempoh (atau untuk sejumlah tempoh) membawa jumlah elektrik yang sama seperti arus berdenyut ini .

Untuk arus ulang alik sinusoidal, nilai Iav bagi setiap tempoh adalah sifar kerana jumlah elektrik yang melalui keratan rentas konduktor dalam satu separuh tempoh adalah sama dengan jumlah elektrik yang melalui arah yang bertentangan semasa separuh tempoh yang lain. Pada graf arus yang menunjukkan pergantungan arus i pada masa t, jumlah elektrik yang dibawa oleh arus dinyatakan dengan luas angka yang dibatasi oleh lengkung semasa, kerana jumlah elektrik ditentukan oleh produk yang ia .

Bagi arus sinusoidal, kawasan separuh gelombang positif dan negatif adalah sama.Dalam arus berdenyut ditunjukkan dalam rajah. 2, dalam tempoh separuh pertama jumlah elektrik yang dibawa oleh komponen AC ditambah kepada jumlah elektrik yang dibawa oleh Iav semasa (kawasan berlorek dalam rajah). Dan semasa kitaran separuh kedua, jumlah elektrik yang sama ditarik balik. Akibatnya, jumlah elektrik yang sama dipindahkan sepanjang tempoh keseluruhan seperti dengan arus terus tunggal Iav, iaitu, luas segi empat tepat Iav T adalah sama dengan kawasan yang dibatasi oleh lengkung arus gelombang.

Oleh itu, komponen malar atau nilai purata arus ditentukan oleh pemindahan cas elektrik melalui keratan rentas wayar.

Persamaan semasa ditunjukkan dalam Rajah. 2 jelas harus ditulis dalam bentuk berikut:

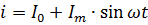
Kuasa arus berdenyut mesti dikira sebagai jumlah kuasa arus komponennya. Sebagai contoh, jika arus ditunjukkan dalam Rajah. 2, melalui perintang rintangan R, maka kuasanya ialah

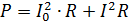
di mana I = 0.7Im ialah nilai rms bagi komponen pembolehubah.

Anda boleh memperkenalkan konsep nilai rms bagi Id arus gelombang. Kuasa dikira dengan cara biasa:

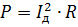
Menyamakan ungkapan ini dengan yang sebelumnya dan mengurangkannya dengan R, kita dapat:

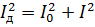
Hubungan yang sama boleh diperolehi untuk tekanan.