Arus ulang alik fasa tunggal

Memperoleh arus ulang alik

Jika wayar A diputar dalam fluks magnet yang dibentuk oleh dua kutub magnet mengikut arah jam (Rajah 1), maka apabila wayar melintasi garisan medan magnet, ia akan mendorong e. d. s yang nilainya ditentukan oleh ungkapan

E = Blvsinα,

di mana B ialah aruhan magnet dalam T, l ialah panjang wayar dalam m, v ialah kelajuan wayar dalam m / s, α — sudut di mana wayar melintasi garisan medan magnet.

Biarkan B, I dan v untuk kes ini kekal malar, maka e teraruh. dan lain-lain. c. akan bergantung hanya pada sudut α di mana wayar melintasi medan magnet. Jadi, pada titik 1, apabila wayar bergerak di sepanjang garis medan magnet, nilai emf teraruh. dan lain-lain. p akan menjadi sifar apabila wayar bergerak ke titik 3 oe. dan lain-lain. v. akan menjadi yang paling penting, kerana garis daya akan dilintasi oleh konduktor ke arah yang berserenjang dengan mereka, dan akhirnya, cth. dan lain-lain. v. sekali lagi akan mencapai sifar jika wayar digerakkan ke titik 5.

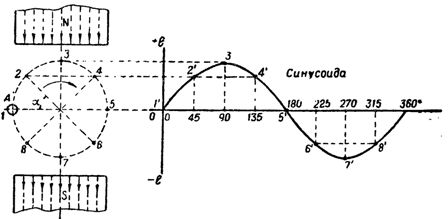
nasi. 1. Menukar induced e. dan lain-lain. ms dalam wayar berputar dalam medan magnet

Pada titik perantaraan 2 dan 4, di mana wayar melintasi garisan daya pada sudut α = 45 °, nilai emf teraruh. dan lain-lain. c. akan bersamaan kurang daripada pada titik 3. Oleh itu, apabila wayar diputar dari titik 1 ke titik 5, iaitu sebanyak 180 °, e teraruh. dan lain-lain. v. berubah daripada sifar kepada maksimum dan kembali kepada sifar.

Ia agak jelas bahawa pada putaran lanjut wayar A melalui sudut 180 ° (melalui titik 6, 7, 8 dan 1), sifat perubahan dalam e teraruh. dan lain-lain. p. akan sama, tetapi arahnya akan berubah ke arah yang bertentangan, kerana wayar akan melintasi garisan medan magnet yang sudah ada di bawah kutub lain, yang bersamaan dengan melintasinya ke arah pertama yang bertentangan.

Oleh itu, apabila wayar diputar 360 °, teraruh e. dan lain-lain. v. bukan sahaja berubah dalam magnitud sepanjang masa, tetapi juga mengubah arahnya dua kali.

Jika wayar ditutup kepada beberapa rintangan maka wayar akan muncul elektrik, juga berbeza dalam saiz dan arah.

Arus elektrik, yang sentiasa berubah dalam magnitud dan arah, dipanggil arus ulang alik.

Apakah gelombang sinus?

Sifat perubahan e. dan lain-lain. (semasa) untuk satu pusingan wayar untuk kejelasan yang lebih besar, ia diwakili secara grafik menggunakan lengkung. Oleh kerana nilai e. dan lain-lain. c. berkadar dengan sinα, maka, setelah menetapkan sudut tertentu, adalah mungkin, dengan bantuan jadual, untuk menentukan nilai sinus setiap sudut, dan pada skala yang sesuai untuk membina lengkung untuk perubahan e. dan lain-lain. c. Untuk melakukan ini, pada paksi mendatar kita akan mengetepikan sudut putaran wayar, dan pada paksi menegak, dalam skala yang sesuai, e teraruh. dan lain-lain. dengan

Jika sebelum ini ditunjukkan dalam rajah.1 sambungkan titik-titik dengan garis melengkung yang licin, maka ia akan memberi gambaran tentang magnitud dan sifat perubahan dalam teraruh e. dan lain-lain. (arus) pada sebarang kedudukan konduktor dalam medan magnet. Disebabkan oleh fakta bahawa nilai teraruh e. dan lain-lain. p. pada bila-bila masa ditentukan oleh sinus sudut di mana wayar melintasi medan magnet yang ditunjukkan dalam rajah. 1 lengkung dipanggil sinusoid, dan e. dan lain-lain. s. - sinusoidal.

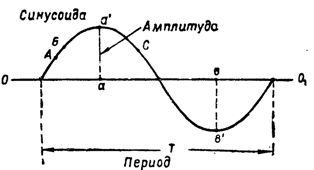
nasi. 2. Sinusoid dan nilai cirinya

Perubahan yang kita lihat e. dan lain-lain. c. sinusoidal sepadan dengan putaran wayar dalam medan magnet pada sudut 360 °. Apabila wayar diputar 360 ° seterusnya, perubahan dalam teraruh e. dan lain-lain. s.(dan arus) akan muncul semula dalam gelombang sinus, iaitu, ia akan berulang secara berkala.

Sehubungan itu, disebabkan oleh ini e. dan lain-lain. c. dipanggil arus ulang alik sinusoidal arus elektrik... Agak jelas bahawa voltan yang boleh diukur oleh kita pada hujung wayar A, dengan adanya litar luar tertutup, juga akan berubah secara sinusoidal.

Arus ulang alik yang diperoleh dengan memutarkan wayar dalam fluks magnet atau sistem wayar yang disambungkan dalam gegelung dipanggil arus ulang alik fasa tunggal.

Arus ulang alik sinusoidal adalah yang paling banyak digunakan dalam teknologi. Walau bagaimanapun, anda boleh menemui arus ulang alik yang tidak berubah mengikut hukum sinus. Arus ulang alik sedemikian dipanggil bukan sinusoidal.

Lihat juga: Apakah itu arus ulang alik dan bagaimana ia berbeza daripada arus terus

Amplitud, tempoh, kekerapan arus ulang alik fasa tunggal

Kekuatan semasa, berubah sepanjang sinusoid, berubah secara berterusan. Jadi, jika pada titik A (Rajah 2) arus adalah sama dengan 3a, maka pada titik B ia sudah menjadi lebih besar.Pada titik lain pada sinusoid, contohnya pada titik C, arus kini akan mempunyai nilai baru, dan seterusnya.

Kekuatan arus pada masa tertentu apabila ia berubah sepanjang sinusoid dipanggil nilai arus segera.

Nilai serta-merta terbesar bagi arus ulang alik fasa tunggal dipanggil apabila ia berubah sepanjang amplitud sinusoidal... Adalah mudah untuk melihat bahawa untuk satu pusingan wayar arus mencapai nilai amplitudnya dua kali. Salah satu nilai aa 'adalah positif dan diambil dari paksi 001 dan satu lagi bv' adalah negatif dan ditarik ke bawah dari paksi.

Masa semasa yang teraruh e. dan lain-lain. (atau daya semasa) melalui keseluruhan kitaran perubahan, yang dipanggil kitaran bulanan T (Rajah 2). Tempoh biasanya diukur dalam beberapa saat.

Timbal balik tempoh itu dipanggil kekerapan (f). Dalam kata lain, frekuensi arus ulang alik ialah bilangan tempoh seunit masa, i.e. dalam secondsdoo. Jadi, sebagai contoh, jika arus ulang-alik dalam masa 1 saat menganggap nilai dan arah yang sama sepuluh kali, maka kekerapan arus ulang-alik tersebut ialah 10 tempoh sesaat.

Untuk mengukur kekerapan, bukannya bilangan tempoh sesaat, unit dipanggil hertz (hertz) digunakan. Kekerapan 1 hertz adalah sama dengan kekerapan 1 lps / saat. Apabila mengukur frekuensi tinggi, lebih mudah untuk menggunakan unit 1000 kali lebih besar daripada hertz, i.e. kilohertz (kHz), atau 1,000,000 kali lebih besar daripada hertz — megahertz (mhz).

Arus ulang alik yang digunakan dalam teknologi, bergantung pada frekuensi, boleh dibahagikan kepada arus frekuensi rendah dan arus frekuensi tinggi.

nilai rms AC

Arus terus yang melalui wayar memanaskannya. Jika anda menjalankan arus ulang alik melalui wayar, wayar juga akan menjadi panas.Ini boleh difahami, kerana walaupun arus ulang alik mengubah arahnya sepanjang masa, pelepasan haba tidak bergantung sama sekali pada arah arus dalam wayar.

Apabila arus ulang alik dialirkan melalui mentol, filamennya akan bercahaya. Pada frekuensi arus ulang-alik standard 50 Hz, tidak akan ada kelipan cahaya, kerana filamen mentol pijar, mempunyai inersia haba, tidak mempunyai masa untuk menyejukkan pada masa-masa apabila arus dalam litar adalah sifar. Penggunaan arus ulang-alik dengan frekuensi kurang daripada 50 Hz untuk pencahayaan kini tidak diingini kerana fakta bahawa turun naik yang tidak menyenangkan dan meletihkan mata dalam keamatan mentol muncul.

Meneruskan analogi arus terus, kita boleh menjangkakan bahawa arus ulang-alik yang mengalir melalui wayar mencipta di sekelilingnya medan magnet. Sebenarnya nArus ulang alik tidak mencipta medan magnet, tetapi kerana medan magnet yang dihasilkannya juga akan berubah-ubah dalam arah dan magnitud.

Arus ulang alik berubah sepanjang masa dalam kedua-dua magnitud dan arahNS. Sememangnya, persoalan timbul tentang cara mengukur pembolehubah T dengan baik, dan apakah nilainya apabila menukar sepanjang sinusoid harus diambil sebagai menyebabkan tindakan ini atau itu.

C Untuk tujuan ini, arus ulang alik dibandingkan dari segi tindakan yang dihasilkannya dengan arus terus, yang nilainya kekal tidak berubah semasa eksperimen.

Katakan arus terus mengalir melalui dawai dengan rintangan malar 10 A dan didapati wayar itu dipanaskan pada suhu 50 °.Jika sekarang kita melalui wayar yang sama bukan arus terus, tetapi arus ulang alik, dan oleh itu kita memilih nilainya (bertindak, sebagai contoh, dengan reostat) supaya wayar juga dipanaskan pada suhu 50 °, kemudian dalam kes ini kita boleh mengatakan bahawa tindakan arus ulang alik adalah sama dengan tindakan arus terus.

Memanaskan wayar dalam kedua-dua kes kepada suhu yang sama menunjukkan bahawa dalam satu unit masa arus ulang alik mengeluarkan dalam wayar jumlah haba yang sama dengan arus terus.

Arus sinusoidal ulang alik yang memancarkan untuk rintangan tertentu per unit masa jumlah haba yang sama dengan arus terus setara dengan magnitud arus terus... Nilai arus ini dipanggil berkesan (Id) atau nilai berkesan arus ulang alik .. . Oleh itu, sebagai contoh kami, nilai berkesan arus ulang alik ialah 10 A... Dalam kes ini, nilai arus maksimum (puncak) akan melebihi nilai purata dalam magnitud.

Pengalaman dan pengiraan menunjukkan bahawa nilai berkesan arus ulang-alik adalah lebih kecil daripada nilai amplitudnya dalam √2 (1.41) kali. Oleh itu, jika nilai puncak arus diketahui, maka nilai efektif arus Id boleh ditentukan dengan membahagikan amplitud arus Ia dengan √2, iaitu Id = Aza/√2

Sebaliknya, jika nilai rms arus diketahui, maka nilai puncak arus boleh dikira, iaitu Ia = Azd√2

Hubungan yang sama akan berlaku untuk amplitud dan nilai rms bagi e. dan lain-lain. v. dan voltan: Unit = Ea /√2, Ud = Uа/√2

Peranti pengukur paling kerap menunjukkan nilai sebenar, oleh itu, apabila notasi, indeks «d» biasanya ditinggalkan, tetapi anda tidak sepatutnya melupakannya.

Impedans dalam litar AC

Apabila pengguna kearuhan dan kemuatan disambungkan ke litar AC, kedua-dua aktif dan reaktans mesti dipertimbangkan (reaktans berlaku apabila kapasitor dihidupkan atau tercekik dalam litar AC). Oleh itu, apabila menentukan arus yang melalui pengguna sedemikian, adalah perlu untuk membahagikan voltan bekalan dengan impedans litar (pengguna).

Impedans (Z) litar AC satu fasa ditentukan oleh formula berikut:

Z = √(R2 + (ωL — 1 / ωC)2

di mana R ialah rintangan aktif litar dalam ohm, L ialah kearuhan litar dalam henries, C ialah kemuatan litar (kapasitor) dalam farad, ω - frekuensi sudut arus ulang-alik.

Pengguna yang berbeza digunakan dalam litar arus ulang-alik di mana ia perlu untuk mempertimbangkan sama ada tiga nilai R, L, C atau hanya sebahagian daripada mereka. Pada masa yang sama, kekerapan sudut arus ulang alik mesti diambil kira.

Bagi sesetengah pengguna, hanya nilai R dan L boleh diambil kira pada nilai kekerapan sudut yang sepadan. Contohnya, pada frekuensi AC 50 Hz gegelung solenoid atau belitan penjana hanya boleh dianggap sebagai mengandungi rintangan aktif dan induktif. Dalam erti kata lain, kapasitansi dalam kes ini boleh diabaikan. Kemudian impedans AC pengguna sedemikian boleh dikira dengan formula:

Z = √(R2 + ω2L2)

Jika gegelung atau gegelung sedemikian direka untuk operasi arus ulang alik disambungkan kepada arus terus voltan yang sama, arus yang sangat besar akan mengalir melalui gegelung, yang boleh membawa kepada penjanaan haba yang ketara, dan penebat gegelung boleh rosak Sebaliknya, arus kecil akan mengalir melalui gegelung yang direka bentuk untuk beroperasi dalam litar arus terus dan disambungkan kepada litar arus ulang-alik voltan yang sama, dan peranti di mana gegelung ini digunakan tidak akan melakukan tindakan yang diperlukan.

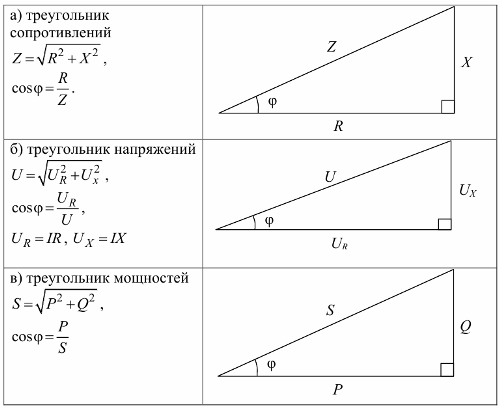
Segitiga rintangan, segitiga voltan dan segi tiga kuasa: